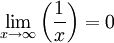¿Cuales son los tipos de Limites?
LIMITES FINITOS
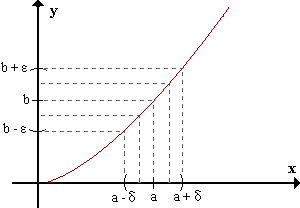
Limf(x)=b <=> para todo ε>0 existe δ>0 / para todo x, 0 < |x-a| < δ |f(x) - b| < ε.
x->a
Otra notación:
limx->a f(x)=b <=> para todo Eb,ε existe un E*a,δ / para todo x perteneciente al E*a,δ f(x) pertenece a Eb,ε.
Se dice que la función f(x) tiene límite b, cuando x tiende a a, si dado ε positivo arbitrario y tan pequeño como se quiera, existe un δ tal que para todo x perteneciente al entorno reducido de a de radio δ, la función pertenece al entorno de b de radio ε.
Dicho de otro modo, para cualquier número positivo ε, por pequeño que sea, podemos encontrar un δ tal que para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) está dentro del entorno de b de radio ε.
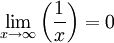
Otra notación:
limx->a f(x)=b <=> para todo Eb,ε existe un E*a,δ / para todo x perteneciente al E*a,δ f(x) pertenece a Eb,ε.
Se dice que la función f(x) tiene límite b, cuando x tiende a a, si dado ε positivo arbitrario y tan pequeño como se quiera, existe un δ tal que para todo x perteneciente al entorno reducido de a de radio δ, la función pertenece al entorno de b de radio ε.
Dicho de otro modo, para cualquier número positivo ε, por pequeño que sea, podemos encontrar un δ tal que para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) está dentro del entorno de b de radio ε.
LIMITES INFINITOS
El símbolo  se lee infinito, es de carácter posicional, no representa ningún número real.
se lee infinito, es de carácter posicional, no representa ningún número real.
Si una variable independiente está creciendo indefinidamente a través de valores positivos, se escribe
está creciendo indefinidamente a través de valores positivos, se escribe  (que se lee:
(que se lee:  tiende a más infinito), y si decrece a través de valores negativos, se denota como
tiende a más infinito), y si decrece a través de valores negativos, se denota como  (que se lee:
(que se lee:  tiende a menos infinito).
tiende a menos infinito).
Si una variable independiente