Valores criticos - Sentido de Concavidad - Criterio de la segunda derivada

Punto Critico

En cálculo, un punto crítico de una función de una variable real es cualquier valor en eldominio en donde la función no es diferenciable o cuando su derivada es 0.

El valor de la función en el punto crítico es un valor crítico de la función. Estas definiciones admiten generalizaciones a funciones de varias variables, mapas diferenciables entre Rm y Rn, y mapas diferenciables entre variedades diferenciables.

Por el teorema de Fermat, los máximos y mínimos locales de una función pueden ocurrir únicamente en sus puntos críticos. Sin embargo, no todo punto estacionario es un máximo o mínimo de la función; puede corresponder también a un punto de inflexión de la gráfica, como para ƒ(x) = x3 en x = 0, o la gráfica puede oscilar en la vecindad del punto, como en el caso de la función definida por la fórmula ƒ(x) = x2sen(1/x) para x ≠ 0 y ƒ(0) = 0, en el punto x = 0.

Sentido de Concavidad

f presenta concavidad positiva en x=a si existe un E*a / para todo x perteneciente al E*a f(x) > f'(a)(x-a) + f(a).
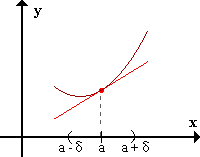La función presenta concavidad positiva en el punto a si, en un entorno reducido de a, la gráfica de f está "por encima" de la recta tangente a f(x) en el punto a.


f presenta concavidad negativa en x=a si existe un E*a / para todo x perteneciente al E*a f(x) < f'(a)(x-a) + f(a).
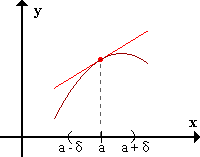La función presenta concavidad negativa en el punto a si, en un entorno reducido de a, la gráfica de f está "por debajo" de la recta tangente a f(x) en el punto a.

Segunda derivada

Derivada segunda

Se llama derivada segunda de una función f(x) a la derivada de la derivada de dicha función.
Notación: f''(x).
Este concepto se puede extender a la derivada n-ésima de una función.

Maximos y Minimos - Absolutos y Relativos - Punto de inflexion

Maximos y Minimos

Definicion: 

Los maximos y minimos de una funcion de dos variables nos permiten medir las altitudes maximas y minimas sobre la superficie que integra la grafica de la funcion (Son parecidas al punto mas alto de una colina y el mas bajo de una hondeada).
Se podria decir que los maximos y los minimos son valores criticos de la funcion donde hay un punto maximo y un punto minimo.

En que consisten

En 1637 Fermat escribió una memoria titulada Methodus ad disquirendam maximan et minimam (“Método para la investigación de máximos y mínimos”). En ella se establecía el primer procedimiento general conocido para calcular máximos y mínimos. Fermat se expresa como sigue.

Toda la teoría de la investigación de máximos y mínimos supone la consideración de dos incógnitas y la única regla siguiente:

1. Sea a una incógnita cualquiera del problema (que tenga una, dos o tres dimensiones, según convenga al enunciado). 2. Se expresará la cantidad máxima o mínima por medio de a en términos que pueden ser de cualquier grado.

3. Se sustituirá a continuación la incógnita original a por a C e, y se expresará la cantidad máxima o mínima por medio de a y e, en términos que pueden ser de cualquier grado. 4. Se “adigualará” para hablar como Diofanto, las dos expresiones de la cantidad máxima o mínima.

5. Se eliminarán los términos comunes de ambos lados, tras lo cual resultará que a ambos lados habrá términos afectados de e o de una de sus potencias. 6. Se dividirán todos los términos por e, o por alguna potencia superior de e, de modo que desaparecerá la e, de al menos uno de los términos de uno cualquiera de los dos miembros. 7. Se suprimirán, a continuación, todos los términos donde todavía aparece la e o una de sus potencias, y se iguala lo que queda, o bien si en uno de los miembros no queda nada, se igualará, lo que viene a ser lo mismo, los términos afectados con signo positivo a los afectados con signo negativo.

8. La resolución de esta última ecuación dará el valor de a, que conducirá al máximo o mínimo, utilizando la expresión original.

Absolutos y Relativos

Maximo Absoluto

Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.

Mínimo absoluto

Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

Maximo y Minimo Relativo
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.

Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
Punto de Inflexion

Un punto de inflexión es un punto donde los valores de x de una función continua pasa de un tipo de concavidad a otra. La curva "atraviesa" la tangente. Matemáticamente la derivada segunda de la función f en el punto de inflexión es cero, o no existe.

En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.

¿Como se Obtiene? 

En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero. Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es. Más concretamente:

1. Se halla la primera derivada de 
2. Se halla la segunda derivada de 
3. Se halla la tercera derivada de 
4. Se iguala la segunda derivada a 0: 
5. Se despeja la variable independiente y se obtienen todos los valores posibles de la misma: .
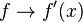
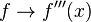
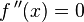
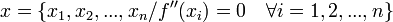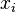6. Se halla la imagen de cada sustituyendo la variable dependiente en la función.
7. Ahora, en la tercera derivada, se sustituye cada :
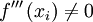   1. Si , se tiene un punto de inflexión en .
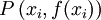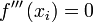   2. Si , debemos sustituir  en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que  no sea nulo, hay que ver qué derivada es:
      1. Si la derivada es impar, se trata de un punto de inflexión.
      2. Si la derivada es par, no se trata de un punto de inflexión.

Pasos de Resolución, Usos y Aplicaciones

DERIVACION

Pasos de resolución:

Paso 1.

Incrementar las 2 variables (Variables X y Y). Acá se les pone el Incremento Delta (∆) representado por un triangulo a cada variable.

Paso 2.

Desarrollar operaciones algebraicas y restarle la función original.Algebraicamente se desarrolla la ecuación (ej. binomios, trinomios) y terminado se le restará la función original al resultado.

Paso 3.

Obtener la razón dividiendo la función incrementada por ∆x. Es decir, dividir cada elemento entre ∆x para así eliminar valores delta (∆x)

Paso 4.

Sustituir ∆x cuando tiende a 0 que es el límite de la función. Sustituiremos todos los ∆x por [0] en toda la ecuación y se multiplicara (Variable multiplicada por 0 da 0)

Usos y Aplicaciones:

El deseo de medir y de cuantificar el cambio, la variación, condujo en el siglo XVII hasta la noción de derivada.

El estudio de las operaciones con derivadas, junto con las integrales, constituyen el cálculo infinitesimal. Los introductores fueron Newton y Leibnitz, de forma independiente. Los conceptos son difíciles y hasta bien entrado el siglo XIX no se simplificaron. A ello contribuyó la aparición de una buena notación, que es la que usaremos. Las aplicaciones prácticas de esta teoría no dejan de aparecer.

Observa la siguiente gráfica y señala en qué intervalos ella crece y decrece.

______________________________________________________________________

Cuando se tiene la gráfica de una función continua resulta bastante fácil señalar en qué intervalo la función es creciente, decreciente o constante. Sin embargo, no resulta fácil decir en que intervalo la función es creciente, decreciente o constante sin la gráfica de la función.

El uso de la derivada de una función puede ayudar a determinar si una función es creciente, decreciente o constante en un intervalo dado. 

Otro claro ejemplo seria; las personas que realizan estadisticas y calculos sobre el tiempo que dura un corredor en una distancia determinada. Eso podria ser parte de una derivacion. 

Practicamente, las derivadas se aplican en trabajos n biología, mecánica, en medicina bacteriológica.

Derivadas

Definición de derivadas, Reglas de Derivadas de Funciones Algebraicas y Reglas de Derivadas de Funciones Trascendentes (Trigonométricas, Exponenciales, Logarítmicas de Base y Naturales).

Derivada

Una derivada puede ser vista como: “Cuanto esta cambiando el valor de una función en un punto dado (o sea su velocidad de variación)”.

Una derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente.

La derivada se presenta como una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia.

Reglas de derivadas de funciones algebraicas

-       La derivada de una constante es igual a 0

Si y=c

y’=0

-       La derivada de una variable independiente es igual a uno (1)

Si y=x

y’=1

-       La derivada del producto de una constante por una variable independiente es igual a la misma constante

Si y=cx

y’=c

-       La derivada de x^n es igual al producto del exponente n por x con exponente disminuido en una unidad

Si y= x^n

y’= nx^n-1

 -        La regla de la cadena es igual al producto del exponente n por su exponente disminuido en una unidad por el producto de la derivada del termino u

Si y= u^n

y’= nu^n-1 d/dx U

-        La derivada de Raiz de n es un cociente cuyo numerador es la derivada de u y el denominador es dos veces la misma raíz.

Si y= √n

y’= d/dx n / 2√u

-        La derivada de la suma de un numero finito de funciones es igual a la suma de las derivadas de las funciones

Si y= u + v + w

y’= d/dx(u) + d/dx(v) + d/dx (w)

-        La derivada del producto de las dos funciones es igual al producto de la primera función por la derivada de la segunda mas el producto de la segunda por la derivada de la primera

Si y= u.v

y’= u d/dx (v) + (v) d/dx u

-        La derivada del cociente de dos funciones es igual al denominador por la derivada del numerador menos el numerador por la derivada del denominado, todo dividido por el cuadrado del denominador

Si y= u / v

y’= v d/dx (u) – (u) d/dx v  / v^2

Reglas de Derivadas de Funciones Trascendentes (Trigonométricas, Exponenciales, Logarítmicas de Base y Naturales)

-       La derivada de seno

Si y= senu

y’= cosu d/dx (u)

-       La derivada de coseno

Si y= cosu

y’= -senu d/dx (u)

-       La derivada de tangente

Si y= tanu

y’= sec^2u d/dx (u)

-       La derivada de Cotangente

Si y= cotu

y’= -csc^2u d/dx (u)

-       La derivada de Secante

Si y= secu

y’= secu.tanu d/dx (u)

-       La derivada de cosecante

Si y= cscu

y’= -cscu.cotu d/dx (u)

-       La derivada de a^u

Si y= a^u

y’= a^ulna d/dx (u)

-       La derivada de e^u

Si y= e^u

y’= e^u d/dx (u)

-       La derivada de Logaritmo Natural (ln)

y= lnu

y’= 1/u d/dx (u)

-       La derivada de logaritmo base logaU

y= logaU

y’=1/Ulna d/dx (u)

Bibliografia 

http://matematica.50webs.com/reglas-de-derivacion.html

http://es.wikipedia.org/wiki/Derivada

https://drive.google.com/folderview?id=0B_JgZqntH5G2X3FDcmhaOUxZaVE&usp=sharing&tid=0B8V6esa6c78BWmdWX0V6bWdsbEk#list